[digital] PLD란?

 

 

PLD(Programmable Logic Device)

• AND array + OR array로 이루어진 IC
• 각 게이트 입력에 퓨즈링크가 연결되어 있다.
• 퓨즈 링크를 전자적으로 연결하거나 끊음으로써 원하는 동작을 하는 조합 논리 함수를 구현할 수 있음

출처 : https://slidesplayer.org/slide/11162137/

 

💡 사용자 요구에 맞게 연결된 상태로 제작하는 것이 아니라, 모든 선이 다 연결된 형태로 제작하는 이유? 
⇒ PLD 제조사는 모든 라인을 연결된 상태로 제공함으로써 동일한 제조 공정으로 PLD를 제작할 수 있다.
(비용, 시간 이득) 
⇒ 사용자는 자신의 설계 요구사항에 맞춰 PLD를 프로그래밍 하여 사용하면 된다! (하드웨어적 유연성)

ex) 논리 함수 F를 GAL로 구현하기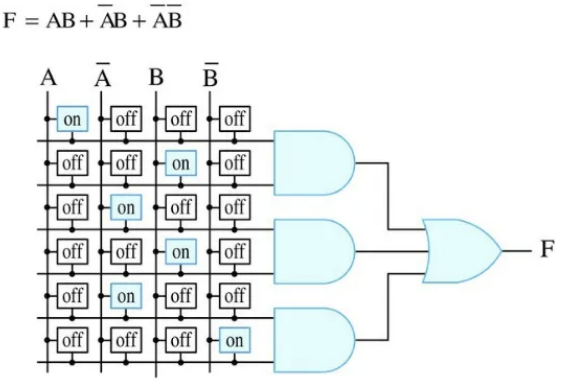

출처 : https://slidesplayer.org/slide/11162137/

 

---

 

왜 AND + OR array 구조일까?

⇒ 모든 부울 함수는 AND + OR 만으로 표현 가능하기 때문이다.

( 📌  AND + OR 만을 통해 표현한 형식을 canonical product / sum 이라 한다.)
⇒ PLD는 AND + OR == SOP 형식 (F = AB + A’B + A’B’)으로 부울 함수를 표현가능하게 해준다.

 

이게 무슨 소리인지 다음을 통해 알아보자!

최소항 (minterm)

• 주어진 변수들이 모두 포함되어 곱의 항으로 나타내어진 것
• N개의 변수 ⇒ 2^N개의 minterm 존재
  • ex) 주어진 변수가 x1, x2, x3라면 minterm 형식은 위와 같다.
• 그 결과가 1인 것을 해당 값의 minterm으로 둔다.
  • ex) x1 = 0, x2 = 0, x3 = 1일 때 minterm m1 = x1’x2’x3
• minterm에 해당하지 않는 다른 모든 mN은 0의 값을 갖는다.
  • ex) (x1x2x3)=(001)일 때, m1을 제외한 모든 mN은 0이다.

 

최대항 (maxterm)

• 주어진 변수들이 모두 포함되어 합의 항으로 나타내어진 것
• 그 결과가 0인 것을 해당 값의 maxterm으로 둔다.
  • ex) x1 = 0, x2 = 0, x3 = 1일 때 maxterm M1 = (x1 + x2 + x3’)
• maxterm에 해당하지 않는 다른 모든 MN은 1의 값을 갖는다.
  • ex) (x1x2x3)=(001)일 때, M1을 제외한 모든 MN은 1이다.

⇒ minterm과 maxterm은 서로 보수 관계이다!

m1 = (x’y’z) ⇒ M1 = m1’ = (x’y’z)’ == x + y + z’

 

 

부울 함수의 표현

• 부울함수 : 불 대수(Boolean Algebra)를 기반으로 하는 함수로, boolean 형식의 입/출력을 가진다.
• 부울함수는 canonical sum / canonical product를 통해 표현할 수 있다.

canonical sum/product

• canonical : 표준적이고 규칙적인 형태
• canonical SOP : 부울 함수를 최소항(Min-term)의 합으로 표현한 형태
• canonical POS : 부울 함수를 최대항(Max-term)의 곱으로 표현한 형태

 

ex) 주어진 입력 A,B에 대해 다음과 같은 출력을 가지는 함수가 있다고 하자

A	B	F(A,B)	minterm	maxterm
0	0	0	m0 = A’B’	M0 = A + B
0	1	0	m1 = A’B	M1 = A + B’
1	0	1	m2 = AB’	M2 = A’ + B
1	1	1	m3 = AB	M3 = A’ + B’

• canonical SOP로 나타내기
  • 최소항으로 나타내기 위해, 결과가 1이 되는 경우를 작성한다. ⇒ m2, m3
  • 결과가 1이 되는 경우 중 하나라도 맞으면 그 결과는 1이므로 합해준다.
    ⇒ F(A,B) = m2 + m3 = AB’ + AB
• canonical POS로 나타내기
  • 최대항으로 나타내기 위해, 결과가 0이 되는 경우를 작성한다. ⇒ M0, M1
  • 결과가 0이 되는 경우가 하나라도 있으면 그 결과는 0이므로 곱해준다.
    ⇒ F(A,B) = M0M1 = (A + B)(A + B’)

💡minterm의 합으로 나타낸 부울 함수를 maxterm으로 나타내고 싶다면, 사용되지 않은 항들의 조합으로 나타내면 된다.
(minterm = 1이 되는 경우를, maxterm = 0이 되는 경우를 통해 표현하므로)

ex) 주어진 입력 x,y, z에 대해(총 8가지 항 존재) F의 SOP형식이 다음과 같다면 
F(x,y,z) = m0 + m3 + m5 + m7 
POS형식은 SOP 형식에서 사용되지 않은 1,2,4,6의 합으로 나타내진다. 
F(x,y,z) = M1M2M4M6

 

부울 함수를 SOP / POS로 나타내면 좋은 점

 

⭐모든 부울함수는 minterm / maxterm의 조합으로 (SOP, POS) 표현될 수 있다.

 

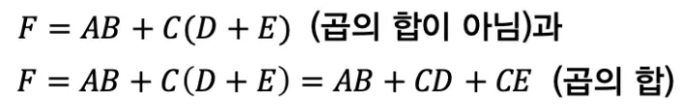
위의 두 식을 논리 게이트로 각각 표현하면 다음과 같다.

 

⇒ 위와 같이 기존 부울 함수를 POS형식으로 나타내 준 경우,

2단계로 회로가 구현되기 때문에 신호 전달 지연시간이 최소화 되며 훨씬 효율적인 회로로 구현할 수 있다.

 

---

PLD를 이용해 부울 함수 구현하기

 

PLD종류

PLD 종류	특징	AND 프로그래밍	OR 프로그래밍
PROM (Programmable ROM)	- 디코더의 역할을 하는 고정 AND 배열과 프로그래밍 가능한 OR 배열로 구성되어 있다. - 주로 주소 지정 메모리로 사용되며 고정된 AND 게이트의 제약 때문에 논리소자로는 사용하지 않는다.	❌	⭕
PLA (Programmable Logic Array)	- AND 입력과 OR 입력 양쪽을 다 프로그래밍할 수 있어서 가장 융통성 있게 프로그래밍 가능. - 동작속도와 집적도가 좀 저하된다.	⭕	⭕
PLE (Programmable Logic Element)	- AND 입력은 고정되고 OR 입력만 프로그래밍할 수 있는 PLD.	❌	⭕
PAL (Programmable Array Logic)	- AND 입력만 프로그래밍할 수 있고 OR 입력은 고정되어 있다. - 현재 가장 널리 쓰이고 있다.	⭕	❌
GAL (Generic Array Logic)	- PLD 중 가장 최근에 개발된 소자. - PAL의 한 가지로 AND 배열만 프로그래밍 가능한 AND 배열과 고정 OR 배열 및 출력핀으로 구성되어 있다. - GAL은 다시 프로그래밍할 수 있고 고도한 출력핀을 프로그래밍할 수 있다.	⭕	❌

 

 

PROM vs PLE

• 공통점 : 고정된 AND, 프로그래밍 가능한 OR 배열을 가진다.
• PROM
  • 특정 입력(주소)에 대한 정해진 결과**(데이터)를 반환**하는 장치
  • 모든 입력 조합을 데이터로 매핑한다.
  • 디코더의 역할을 한다
  • 입력(N bit)에 대해 모든 가능한 조합 (2^N개)을 AND에서 반환한다. ⇒ 모든 가능한 최소항 m0 ~ m(2^N)반환함
• PLE
  • 조립 가능한 블록처럼 특정 입력을 통해 논리식을 구성하며, 더 많은 논리적 유연성을 제공
  • 필요한 입력 조합만 결합하여 논리식 생성
  • 모든 가능한 최소항을 생성하지 않는다.
  • 설계자가 필요한 입력 조합만 선택적으로 사용한다.

항목	PROM	PLE
목적	데이터를 저장하고 읽기 위한 메모리	논리식을 구현하는 디지털 논리 소자
사용 초점	주소 지정 및 데이터 반환	논리 연산 구현 및 디지털 제어
AND 배열	디코더 역할 (고정된 주소 매핑)	논리식 조합의 입력 생성 (고정)
OR 배열	데이터 반환을 위한 출력 프로그래밍	논리식 출력을 생성하기 위한 프로그래밍
유연성	논리 설계 유연성 낮음	PROM보다는 논리 설계 유연성 높음
응용 분야	메모리 칩, 주소 디코딩	제어 논리, 디지털 시스템 설계

 

 

---

 

PLA

• AND 입력과 OR 입력 양쪽을 다 프로그래밍할 수 있음
• 양쪽 다 퓨즈가 연결되어 있기 때문에 유연성은 높지만 집적도가 낮고, 동작 속도가 느리다.

---

 

PAL

• 프로그래밍 가능한 AND, 고정된 OR 배열을 가진다.
• 가장 많이 쓰이는 PLD 종류이다.
• 위와 같은 PAL이 있다고 할 때, 해당 PAL는 다음과 같이 고정된 OR Array 출력을 가진다.

• 따라서, AND array를 프로그래밍 하여 각 입력에 대해 원하는 출력이 나오도록 Gate를 minterm 형식으로 구현해주면 된다. 예를 들어, G0은 다음과 같이 프로그래밍 되어 있다.

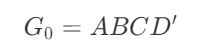
💡 PAL은 왜 PLD중 가장 많이 사용될까?

1. 단순한 구조
=> 양쪽 다 프로그래밍 가능한 PLA에 비해 하드웨어 설계가 더 간단하고, 동작 속도가 빠르다.

2. 높은 유연성
=> PLE는 가능한 minterm 형식의 제약이 있기 때문에 사용 가능한 Product 논리식의 종류가 제한되는 반면, PAL는 설계자가 원하는 모든 minterm을 구현할 수 있기 때문에 더 유연하게 기능을 구현할 수 있다. 

 

---

 

📌 GAL(Generic Array Logic)

출처 : https://slidesplayer.org/slide/11162137/

특징	PAL (퓨즈 구조)	GAL (E²CMOS 셀 구조)
재프로그래밍	비가역적 (한 번만 프로그래밍 가능)	가역적 (재프로그래밍 가능)
유연성	설계 변경이 불가능	설계 변경 및 수정이 용이
비용	비용이 낮음	비용이 다소 높음
전력 소모	상대적으로 낮음	E²CMOS 셀로 인해 약간 높음
내구성	높은 내구성	반복적인 프로그래밍에 따른 한계 존재
응용 범위	고정 설계, 단순 논리회로	프로토타이핑, 설계 수정이 필요한 응용

• 퓨즈 : 초기에는 연결상태이며, 특정 전압을 가하면 물리적으로 끊어지게된다. (해당 라인 비활성화)
• E2CMOS (Electrically Erasable CMOS) : 전기적으로 지울 수 있는 CMOS. 특정 전압을 가해 끊거나 연결 할 수 있다. (재프로그래밍 가능)